Units, Scalars and Vectors: An Over Simplified Primer
Why units?
In science your numbers need units (grams, meters, liters, seconds…). These units combined with your numbers provide information on a measurement. If asked how much water is in the graduated cylander you wouldn’t say 20, you need to describe 20 of what (hopefully milileters).
For an anaolgy of the units I think you could consider them as an adjective (though out of order): loud+music tells you a relative intensity of what you are listening to. Hot surface implies you don’t want to touch the surface.
Physics and units
Let’s take a moment and consider three of the units I mentioned earlier: grams (g), meters (m), seconds (s). I’m assuming its under stood in SI units there are pre-fixes (milli, kilo, nano to make a few) and will not go into them. But these four units encompass the first bit of intro physics. Breaking them down though:
- grams: unit for mass (not weight). Where mass describes the amount of matter within an object
- meters: unit for “length”. A measurement of how far you’ve gone, how long something is
- seconds: unit for time. A measurment between two events, or how long something may last
Now in physics there are some caveats. The standard unit for mass in physics is kilogram (kg). And while second is standard, hours are also frequently used (1 hour = 3600 seconds).
Second many of these usits can be combined to tell you more information. Something I noticed when I was a tutor was when units were combined, students seemed initially overwhellmed. I’m going to provide a little table to look at a few of them:
| Unit1 | Unit 2 | New Unit | definition |
|---|---|---|---|
| m | s | m/s (speed) | How does the distance change with time (how fast are you going) |
| m/s | s | m/s^2 (acceleration) | How does the speed change with time (how fast are you chaning speeds) |
| kg | m/s^2 | Kg * m/s^2 = N (Force) | What acceleration needs to be applied to move an object (or how much does an object weigh) |
| kg | (m/s)^2 | Kg * (m/s)^2 = J (Energy) | The capacity to do work (Force * displacement) |
| N | m | N * m = J (Energy) | The capacity to do work (Force * displacement) |
Scalars and Vectors
What’s the difference?
So I’ve text vomited about units. Without units you don’t have information on what is being measured. In physics (as well as math) you can take numbers a step further with scalars and vectors.
A scalar is really what I have been talked about, its a number with a unit describing a measurement. I drove 30 km and another 30 km back.
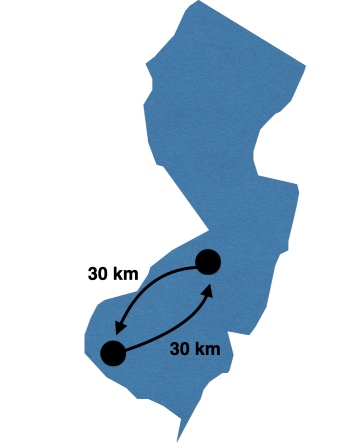
Any two like scalars (they have the same units) can be summed together and should produce a larger number (so this person drove 60 km).
A vector is a number with a unit and a direction and you can ONLY add vectors that share an axis (x to x and y to y if you will), and like scalars, only like units can be added together (force in x with force in x). The image below for example. I cannot add the north pointing arrow and the east pointing arrow together! They are on different axis.
Vectors do not apply to all measurments: mass, energy, and time cannot have a direction for example. You can talk about the mass in a location (weight distribution), that is not the same as mass is pointing in “that” direction however.
Catagorizing Scalars and Vectors
The question I used to be asked was well what is a vector then?!?! I used to look at the students dumbfounded in part because it’s a good question, in part you need slightly more math do explain (that is not happening here).
For the moment lets list the scalars that cannot be anything burt a scalar from the units I’ve thrown at you:
- time
- mass
- energy
These are scalars no mater what, the do not have a direction associated with them. What’s that leave us with? Units for speed, acceleration, length, force. Well which is a scalar and which is a vector?
Vectors
Let’s look at a vector. In 2D (drawing on a map for example) a vector has a x (left/right) and a y (up/down) direction.
Lets start with a simple example using the map of NJ. We will define one axis that goes where north east is positive and south west is negative.
You travel from Haddon Heights to Carney’s Point. It’s about 30 km south west (3000m), and back another 30 km north east.

The “vectorized” version of distance is called displacement.
NOW, remember, a vector has both a value and a direction. Here south-west will be considered going in a negative direction, while north-east are a postive direction.
You travel 30 km south west (where south west is the direction). On your way back you travel 30 km north east. Adding the two displacements together will sum to 0 km!
Now in intro physics you’ll tend to work with x, y, and z instead of north, south, east and west.
Scalar and Vector Overlap
| At this point you may be asking, and rightly so, why do some scalars and some vectors units overlap? And the answer is any vector can be written as a scalar if you take the magnituded of the vector. For the moment don’t worry about how we do that, note that anything written between two | is the magnitude. Four examples are below. |
| Unit | Scalar | Vector |
|---|---|---|
| m | |Displacement| = Distance | Displacement |
| m/s | |Velocity| = Speed | Velocity |
| m/(s^2) | |Acceleration| | Acceleration |
| N | |Force| | Force |
Drawing Vectors
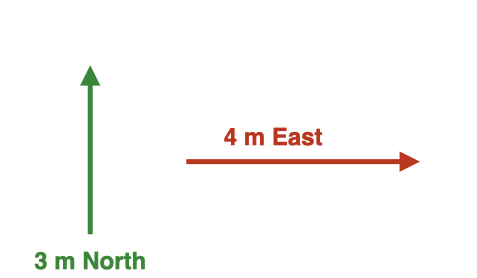
Lets start with drawing a vector one peice at a time on a x-y plane. Vectors will be described as colored arrow on either an x or y axis. The goal here is to track how an individual walked. We start with a displacement in y, where some one has walked 3m in the positive y direction.
Now from the point left off, we walk 4m’s in the positive x direction
Lets now draw the two vectors together. Doing this we see a clear picture of how we’ve travled, and in what direction! This example can be extended to be used for ANY vector: forces, velocities…
NOW, if we want to calculate a distance (the scalar) of the vectors show directly above:
The distance is the squareroot of sum of both vectors squared. For any vector, you can find the magnitude by taking the square root of the the square sum of vectors for that measurement.
Now remember this, any scalar cannot be plotted like a vector. I cannot plot energy’s direction because it has no direction.